Blog
最近ローソンでお菓子をたくさん買った田中です。
近頃読んで面白かった論文を紹介したいと思います。
A Play on Regular Expression今年のICFPでFunctional Pearlとして発表されたものです。ICFP(International Conference on Functional Programming)というのは、関数プログラミングに関する国際学会で、Functional Pearlというのは、エレガントでためになる、関数プログラミングのテクニック集です。
この論文ではまず、正規表現マッチャを関数型言語(Haskell)でいかにエレガントに記述できるかが示されます。それから、エレガントさを保ったままの線形時間実装へ改良し、その実装がC++によるプロフェッショナルな実装(具体的にはGoogle re2)に匹敵するパフォーマンスを示すことが示されます。さらにそれだけでなく、遅延評価の力を用いて、正規言語を超える、すなわち(正規表現なのに!)任意の文脈自由言語がマッチできるように改良されます。
余談ですが、タイトルに”A Play”とあるように、この論文は、全編演劇の台本風に書かれています。それ自体読んでいてなかなか楽しいものですので、興味を持たれましたら原文も読まれることをおすすめします。
正規表現マッチャを実装する
正規表現マッチャを実装するにあたって、まずは正規表現の内部表現を定義します。正規表現とはなんぞや、というのは、おおよそ皆さん十分ご存知かと思いますので、細かい説明は割愛させていただきます。一口に正規表現と言いましても、posix、perlの実装、様々な拡張がありますが、ここでは拡張を含まない、正規言語を記述できるもの、とします。
正規言語とは以下のように再帰的に定義される集合です。
- 空文字列 ε は正規言語である
- アルファベット a は正規言語である
- A と B が正規言語であるとき、A|B(和集合)、AB(結合)、A*(クリーネ閉包)も正規言語である
これをそのままHaskellのデータ構造として表現すると以下のようになります。
data Reg = Eps -- ε
| Sym Char -- a
| Alt Reg Reg -- A|B
| Seq Reg Reg -- AB
| Rep Reg -- A*
例えば、(アルファベット{a, b, c}上で)偶数個の c を含むという正規表現
((a|b)*c(a|b)*c)*(a|b)*
をRegで表すと、
let nocs = Rep (Alt (Sym 'a') (Sym 'b')) in let onec = Seq nocs (Sym 'c') in Seq (Rep (Seq onec onec)) nocs
となります。
さて、これに対してマッチ関数を書きます。
accept :: Reg -> String -> Bool accept Eps u = null u accept (Sym c) u = u == accept (Alt p q) u = accept p u || accept q u accept (Seq p q) u = or [accept p u1 && accept q u2 | (u1, u2) <- split u] accept (Rep r) u = or [and [accept r ui | ui <- ps] | ps <- parts u]
split関数は、与えられた文字列を二つに切り分ける全パターンのリストを返し、parts関数は、与えられた文字列を任意の個数に切り分ける全パターンのリストを返す関数です。それぞれの定義は次のように定義できます。
split :: [a] -> [([a], [a])] split [] = [([], [])] split (c:cs) = ([], c:cs) : [(c:s1, s2) | (s1, s2) <- split cs] parts :: [a] -> [[[a]]] parts [] = [[]] parts = [[c]] parts (c:cs) = concat [[(c:p):ps, :p:ps] | p:ps <- parts cs]
完成しました。とてもシンプルでエレガントな実装ですが、切り分け方を全パターン試していたり、Altにおいてバックトラックが発生するので、この実装では入力長に対して最悪指数時間かかってしまいます。
重みを付ける
速度のことはひとまず置いておいて、機能の拡張を考えます。先程の実装では、文字列全体が正規表現にマッチしたかどうかしか分かりません。accept関数では正規表現と文字列に対して、Boolを返していました。Boolの代わりに半環(Semiring)を用いることを考えます。半環を用いると、マッチしたかどうかの他に、全マッチ数、マッチ位置、最左最長マッチなどが”同じアルゴリズムで”計算できるようになります。半環とは、”加法”と”乗法”と呼ばれる二種類の二項演算によって定まる代数的構造です。
加法(+)、乗法(*)の二つの二項演算と、二つの元0、1に対して次の法則が成り立ちます。
- 加法に関して交換法則と、0が単位元
- (a + b) + c = a + (b + c)
- 0 + a = a + 0 = a
- a + b = b + a
- 乗法に関して交換法則と、1が単位元
- (a * b) * c = a * (b * c)
- 1 * a = a * 1 = a
- 分配法則
- a * (b + c) = (a * b) + (a * c)
- (a + b) * c = (a * c) + (b * c)
- 乗法に関して、0が零元
- 0 * a = a * 0 = 0
半環をHaskellの型クラスとして表現すると、次のようになります。
class Semiring s where zero :: s one :: s (<+>) :: s -> s -> s (<*>) :: s -> s -> s
例えば、BoolはSemiringのインスタンスにすることができます。
instance Semiring Bool where zero = False one = True (<+>) = (||) (<*>) = (&&)
IntもSemiringのインスタンスにできます。
instance Semiring Int where zero = 0 one = 1 (<+>) = (+) (<*>) = (*)
これらは上記の法則を満たしています。また、それを満たすようにするのはプログラマの責任です。
さて、マッチで半環を返せるようにするために、Regを修正します。
data RegW c s = EpsW
| SymW (c -> s)
| AltW (RegW c s) (RegW c s)
| SeqW (RegW c s) (RegW c s)
| RepW (RegW c s)
RegWはパラメータとして、文字型cと半環型sを取るようになって、SymWは関数を取るようになりました。SymはCharを引数に取っていましたが、これは暗黙的に、x -> if x == c then True else False という関数を表していました。関数を明示的に取るようにすることによって、任意の文字にマッチする正規表現などが簡単に表せるようになるなど、より柔軟になります。
文字に対するSymWを楽に構築するためのヘルパ関数を作っておきます。
sym :: Semiring s => Char -> RegW Char s sym c = SymW (x -> if x == c then one else zero)
また、Regを自動的にRegWに変換する関数が書けます。
weighted :: Semiring s => Reg -> RegW Char s weighted Eps = EpsW weighted (Sym c) = sym c weighted (Alt p q) = AltW (weighted p) (weighted q) weighted (Seq p q) = SeqW (weighted p) (weighted q) weighted (Rep p) = RepW (weighted p)
RegWが定義できたので、これに対するaccept関数を書きます。
acceptW :: Semiring s => RegW c s -> -> s acceptW EpsW u = if null u then one else zero acceptW (SymW f) u = case u of -> f c; _ -> zero acceptW (AltW p q) u = acceptW p u <+> acceptW q u acceptW (SeqW p q) u = sum [acceptW p u1 <*> acceptW q u2 | (u1, u2) <- split u] acceptW (RepW r) u = sum [prod [acceptW r ui | ui <- ps] | ps <- parts u]
先程のaccept関数とほぼ同じです。&&が<*>に、||が<+>に、Trueがoneに、Falseがzeroに変わっています。また、orがsumに、andがprodに変えられました。これらは、Semiring上でのorとandで、定義は次の通りです。
sum, prod :: Semiring s => [s] -> s sum = foldr (<+>) zero prod = foldr (<*>) one
実際に試してみます。
ghci> let as = Alt (Sym 'a') (Rep (Sym 'a')) ghci> acceptW (weighted as) "a" :: Int 2 ghci> acceptW (weighted as) "a" :: Bool True ghci> acceptW (weighted as) "a" :: Int 0 ghci> acceptW (weighted as) "b" :: Bool False ghci> let bs = Alt (Sym 'b') (Rep (Sym 'b')) ghci> acceptW (weighted (Seq as bs)) "ab" :: Int 4
SemiringのインスタンスであるBoolとIntに対して、全く同じコードが動作して、それぞれマッチしたかとマッチ数を計算できています。
マッチングの高速化
acceptW関数はバックトラックを用いているために、最悪の場合計算に指数時間かかります。”(a|ε){n}a{n}” ({n}はn回の繰り返しを表す) という正規表現に対してn個のaからなる文字列をマッチさせることを考えます。この正規表現は、nから2n個のaからなる文字列にマッチするので、n個のaからなる文字列はマッチします。しかし、マッチするには前半部分において、すべてε側が選ばれなければなりません。そのため、バックトラックを用いる実装だとnに対して指数時間かかってしまう可能性があります。
例えばgrepコマンドの正規表現だと、このように遅くなっていきます。
$ time for i in `seq 1 200`; do echo -n a; done | grep -cE "^(a?){200}a{200}$"
1
real 0m0.383s
user 0m0.186s
sys 0m0.075s
$ time for i in `seq 1 400`; do echo -n a; done | grep -cE "^(a?){400}a{400}$"
1
real 0m2.252s
user 0m2.186s
sys 0m0.015s
$ time for i in `seq 1 800`; do echo -n a; done | grep -cE "^(a?){800}a{800}$"
1
real 0m30.568s
user 0m30.420s
sys 0m0.107s
正規表現のマッチングには、入力長に対して線形時間のアルゴリズムが知られています。正規言語は決定性・非決定性有限オートマトン(DFA・NFA)によって受理できるので、まず正規表現をDFAに変換して、それからDFAを用いてマッチングを行うと、線形時間でマッチングすることができます。
しかし、DFAは正規表現のサイズに対して指数サイズになる場合があります。例えば、
(a|b)*a(a|b){n}a(a|b)*
という正規表現がその例です。これはn文字離れたところに2つのaがある時マッチするという正規表現です。これのDFAがなぜ指数サイズになるのか直感的な説明をします。n個離れた場所にaがあるということを判断するためには、直前n個の履歴が必要になります。直前n個の履歴はアルファベットが2種類の時、2^n通りあります。これをオートマトンで表現するには状態が2^n個必要になるというわけです。
DFAが指数サイズになるとしても、その状態のうち実際に到達するのは最大でも入力長個しかありません。ということは、DFAをオンザフライで構築しながらマッチングすれば、実際に構築するDFAの状態数は入力長以下のサイズで済むということになります。
DFAをオンザフライで構築するのは簡単ではないのですが、NFAを用いると容易に同等のことができます。全ての到達可能なNFAの状態の集合をDFAの状態として計算すればいいのです。
これを普通に実装しようとすると、まず正規表現からNFAを生成して、それからマッチングを行うというようになると思います。しかし、ここで少し考えてみます。NFAでの状態というのは実は元の正規表現のノードにそれぞれ対応しています。つまり、正規表現のノードをマークしていけば、NFAをシミュレートするのと同様のことができます。
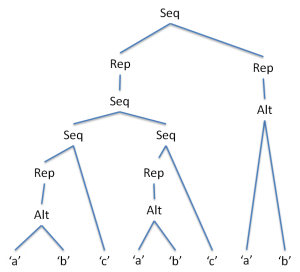
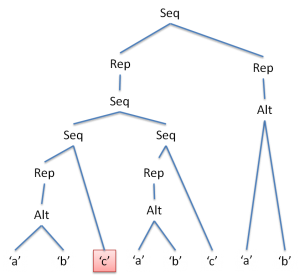
例えば、先に挙げた、cを偶数個含む文字列を表す正規表現
((a|b)*c(a|b)*c)*(a|b)*
これをツリーで表すと、このようになります。
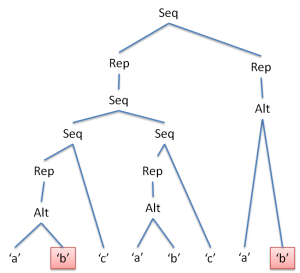
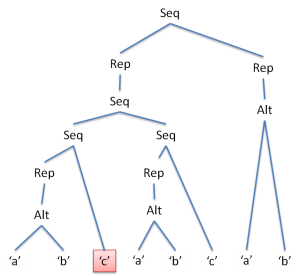
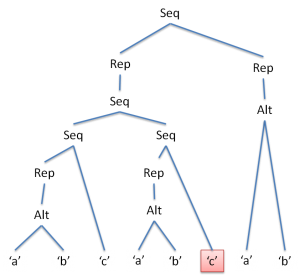
これに対してbcccを入力すると、次の図のようにマークされていきます。
このように、ノードにフラグを一つ加えてやるだけで、正規表現のままでNFAをシミュレートするのと同様に、線形時間マッチが可能になります。
まず、そのように拡張された正規表現の型を定義します。ひとまず今は重みのことは忘れておきます。
data REG = EPS
| SYM Bool Char
| ALT REG REG
| SEQ REG REG
| REP REG
SYMのところにBoolが増えています。これがマッチしているかを示すマークです。
1文字入力するごとに、新しい位置がマークされた正規表現を返します。そのための1ステップの計算を行う関数shiftを定義します。
shift :: Bool -> REG -> Char -> REG
shift _ EPS _ = EPS
shift m (SYM _ x) c = SYM (m && x == c) x
shift m (ALT p q) c = ALT (shift m p c) (shift m q c)
shift m (SEQ p q) c =
SEQ (shift m p c)
(shift (m && empty p || final p) q c)
shift m (REP r) c = REP (shift (m || final r) r c)
第一引数のBoolはマークできるかを表しています。あるノードをマークするためには、そのノードの直前に位置する可能性のあるいずれかのノードがマークされていなければなりません。すなわち引数mは、直前に位置する可能性のあるノードのいずれかがマークされているかを表します。
SEQの右手側について、マークできるかどうかの条件がやや複雑です。mがTrueで、かつpが空文字列を受理する可能性があるなら、qの直前がマークされている可能性があるのでqはマークできます。あるいは、pのラストに位置する可能性のあるノードのいずれかがマークされている場合も、qの直前がマークされているということになるので、qはマークできます。REPに関しても同様です。
shift中に出てくるempty、finalの関数は、それぞれ正規表現が空文字列を受理する可能性があるか、最後に位置する可能性のあるノードのいずれかがマークされているかを返します。それぞれ定義は次のとおりです。
empty :: REG -> Bool empty EPS = True empty (SYM _ _) = False empty (ALT p q) = empty p || empty q empty (SEQ p q) = empty p && empty q empty (REP r) = True final :: REG -> Bool final EPS = False final (SYM b _) = b final (ALT p q) = final p || final q final (SEQ p q) = final p && empty q || final q final (REP r) = final r
最後にマッチ関数を書きます。これは、入力毎に正規表現を更新していくので、foldlがぴったりです。
match :: REG -> String -> Bool match r [] = empty r match r (c : cs) = final (foldl (shift False) (shift True r c) cs)
1文字目が入力されるとき、正規表現はどこもマークされていないので、先頭に位置するノードがマークできるように、shiftにTrueを渡します。二文字目以降は既にマークされているノードの後続しかマークしてはいけないのでFalseを渡します。最後に、末尾に来るノードがマークされているかどうかをfinalで調べます。
さて、これで線形時間のマッチができたでしょうか?少し不十分なところがあります。それはSEQのshiftのところで、shift m p c、empty p、final p と3回 p をトラバースしているところです。これを何とかしなければいけません。empty及びfinalはREGに対して一意に決まる値なので、キャッシュしておけば、定数時間で取り出すことができます。
data REGW c s = REGW { emptyW :: s,
finalW :: s,
regW :: REW c s }
data REW c s = EPSW
| SYMW (c -> s)
| ALTW (REGW c s) (REGW c s)
| SEQW (REGW c s) (REGW c s)
| REPW (REGW c s)
REGにemptyとfinalを持たせ、さらにSemiringに対応しました。REGWに対応させたマッチャは次のようになります。
epsW :: Semiring s => REGW c s
epsW = REGW { emptyW = one,
finalW = zero,
regW = EPSW }
symW :: Semiring s => (c -> s) -> REGW c s
symW f = REGW { emptyW = zero,
finalW = zero,
regW = SYMW f }
altW :: Semiring s => REGW c s -> REGW c s -> REGW c s
altW p q = REGW { emptyW = emptyW p <+> emptyW q,
finalW = finalW p <+> finalW q,
regW = ALTW p q }
seqW :: Semiring s => REGW c s -> REGW c s -> REGW c s
seqW p q =
REGw { emptyW = emptyW p <*> emptyW q,
finalW = finalW p <*> emptyW q <+> finalW q,
regW = SEQW p q }
repW :: Semiring s => REGW c s -> REGW c s
repW r = REGW { emptyW = one,
finalW = finalW r,
regW = REPW r }
matchW :: Semiring s => REGW c s -> -> s
matchW r [] = emptyW r
matchW r (c : cs) =
finalW (foldl (shiftW zero . regW) (shiftW one (regW r) c) cs)
shiftW :: Semiring s => s -> REW c s -> c -> REGW c s
shiftW _ EPSW _ = epsW
shiftW m (SYMW f) c = (symW f) { finalW = m <*> f c }
shiftW m (ALTW p q) c =
altW (shiftW m (regW p) c) (shiftW m (regW q) c)
shiftW m (SEQW p q) c =
seqW (shiftW m (regW p) c)
(shiftW (m <*> emptyW p <+> finalW p) (regW q) c)
shiftW m (REPW r) c =
repW (shiftW (m <+> finalW r) (regW r) c)
emptyWとfinalWを、REGW構築時に計算してしまいます。そのようなepsW、symW、altWをスマートコンストラクタと呼んだりします。
さてこれで、線形時間の正規表現マッチャが完成しました。コードは依然として短く、簡潔です。
重みの改良
現在マッチの結果はSemiringで、BoolとIntがSemiringのインスタンスになっていて、それぞれ、マッチしたかどうか、マッチ総数を得ることができます。一般的な正規表現マッチャでは、マッチした位置や区間が得られます。そのような情報が得られるような重みを作ることができるでしょうか?
それはこのままでは無理です。というのも、マッチャが文字の出現位置を知る手段が無いからです。そこで、入力として文字列、即ち文字のリストを与える代わりに、位置情報をzipした[(Int, c)]を与えるように変更します。
また、部分マッチというものを考えなければいけません。今までは与えられた文字列全体がマッチしているかどうかをチェックしていましたが、これを部分文字列へのマッチに対応させる必要があります。これは簡単で、単に与えられた正規表現の前後に “.*” を付ければよいです。さて、そのような部分マッチ関数を書きます。
submatchW :: Semiring s => REGW (Int, c) s -> -> s submatchW r s = matchW (seqW arb (seqW r arb)) (zip [0..] s) where arb = repW (symW (_ -> one))
arb が正規表現 “.*” に対応しています。SYMWが文字から重みへの関数を取るようになっているので、すべての文字にマッチするようなパターンが簡単に書けます。
もう一つ拡張しなければならない点として、位置情報のIntからSemiringへの変換があります。そのために新しくSemiringIクラスを作ることにします。
class Semiring s => SemiringI s where index :: Int -> s
sym関数をSemiringIに対応させます。
symI :: SemiringI s => Char -> REGW (Int, Char) s
symI c = symW weight
where weight (pos, x) | x == c = index pos
| otherwise = zero
さてこれで位置対応の部分マッチが完成しました。あとは、SemiringIのインスタンスを作るだけです。まずは最左マッチの位置を返すSemiringを作ります。
data Leftmost = NoLeft | Leftmost Start data Start = NoStart | Start Int
NoLeftはSemiringのzeroに相当します。Leftmost NoStartはoneに相当しますが、これは空文字へのマッチなど、位置情報がない場合を表します。
instance Semiring Leftmost where
zero = NoLeft
one = Leftmost NoStart
NoLeft <+> x = x
x <+> NoLeft = x
Leftmost x <+> Leftmost y = Leftmost (leftmost x y)
where leftmost NoStart NoStart = NoStart
leftmost NoStart (Start i) = Start i
leftmost (Start i) NoStart = Start i
leftmost (Start i) (Start j) = Start (min i j)
NoLeft <*> _ = NoLeft
_ <*> NoLeft = NoLeft
Leftmost x <*> Leftmost y = Leftmost (start x y)
where start NoStart s = s
start s _ = s
instance SemiringI Leftmost where
index = Leftmost . Start
LeftmostをSemiring、SemiringIのインスタンスにします。加法は、どちらかに位置情報があればそれを、両方にある場合は最左なので、minを取ります。乗法は片方しかない場合はNoLeftを、両方ある場合は左を返します。左がNoStartなら右を返します。
LeftmostがSemiringになりました。これで、先程と全く同じアルゴリズムで、最左マッチが求められるようになりました。
ghci> let a = symI 'a' ghci> let ab = repW (a `altW` symI 'b') ghci> let aaba = a `seqw` ab `seqw` a ghci> submatchW aaba "ab" :: Leftmost NoLeft ghci> submatchW aaba "aa" :: Leftmost Leftmost (Start 0) ghci> submatchW aaba "bababa" :: Leftmost Leftmost (Start 1)
位置だけでなく、区間を取りたい場合はどうでしょう。最左最長マッチの区間を取る重みを考えてみます。基本的には最左マッチと同じです。
data LeftLong = NoLeftLong | LeftLong Range
data Range = NoRange | Range Int Int
instance Semiring LeftLong where
zero = NoLeft
one = LeftLong NoRange
NoLeftLong <+> x = x
x <+> NoLeftLong = x
LeftLong x <+> LeftLong y = LeftLong (leftlong x y)
where leftlong NoRange NoRange = NoRange
leftlong NoRange (Range i j) = Range i j
leftlong (Range i j) NoRange = Range i j
leftlong (Range i j) (Range k l)
| i < k || i == k && j >= l = Range i j
| otherwise = Range k l
NoLeftLong <*> _ = NoLeftLong
_ <*> NoLeftLong = NoLeftLong
LeftLong x <*> LeftLong y = LeftLong (range x y)
where range NoRange s = s
range (Range i _) (Range _ j) = Range i j
instance SemiringI LeftLong where
index i = LeftLong (Range i i)
LeftLongをSemiringに出来ました。これで、またもや先ほどと全く同じアルゴリズムで、最左最長マッチを求められるようになりました。
ghci> submatchw aaba "ab" :: LeftLong NoLeftLong ghci> submatchw aaba "aa" :: LeftLong LeftLong (Range 0 1) ghci> submatchw aaba "bababa" :: LeftLong LeftLong (Range 1 5)
実験
さてここまでで、非常にシンプルでエレガントで入力長に対して線形時間な正規表現マッチャが書けたのですが、実際のところこの実装はどうなのでしょうか?unix上での一般的な正規表現マッチツールのgrepと、最新のC++によるプロフェッショナルな実装(Googleのre2)との比較を行ってみます。
まずは、先ほど挙げた正規表現 “^(a?){n}a{n}$” で比較してみます。この正規表現はaがn文字から2n文字の文字列に対してマッチしますが、ちょうどn文字に対してマッチさせるには a? の部分で全て空文字を選ばねばならず、バックトラック実装では指数時間かかってしまいます。
$ time for i in `seq 1 500`;do echo -n a;done | grep -cE "^(a?){500}a{500}$"
1
real 0m17.235s
user 0m17.094s
sys 0m0.059s
同様の正規表現を、Haskellの実装とre2で処理すると、それぞれ0.06秒、0.09秒でした。両者とても速いのでもう少し大きい入力を与えます。入力を5000文字にすると、それぞれHaskell 21.19秒、re2 4.919秒という結果になりました。Haskellの方が5倍遅いですが、プロファイルを取ってみると、GCに掛かっている時間が8割以上を占めていることが分かります。Haskellの実装では、1文字ごとに正規表現全体が更新され、新しい文字が入力されると前の正規表現は即座にゴミになるので、GCに時間がかかっているものと思われます。これは今のままのやり方ではいかんともしがたそうです。
次に、DFAサイズが指数的になる例、”.*a.{n}a.*” (nは任意の整数)を試してみます。n=20で試します。入力はランダムに、かつマッチしないように生成された文字列1000000文字です。Haskell版が3.10秒、re2が4.43秒という結果になりました。今回は、正規表現のサイズが小さいので、GCにほとんど時間がかからず高速でした。
(補足:上記実験結果は論文よりの引用です。手元で実験してみたところ、非常に遅く、かつ大量にメモリを食っていました(前者500文字で2秒、5000文字でメモリ溢れで計算できず)。これはmatchW関数が正規表現を生成する際、遅延評価の為に1文字毎に不要になった正規表現がごみになること無く、最後まで回収されないのが原因のようでした(論文のケースではコンパイラの正確性解析がうまく行ったということでしょうか。ただ、このままのコードではうまくいかないように思います)。そこで、REGWをNFDataクラスのインスタンスにして正規表現をStrictに計算できるようにし、foldlをやめて1ステップごとに正規表現をrnf(normal formになるまで評価)するように変更したところ、メモリ使用量が一定になり、速度も大幅に改善されました(2秒→0.4秒)。しかし、それでも論文程の性能は出ませんでした。2つ目の正規表現に関してはほぼ同等の速度が出ました。論文で実験に用いられた実装には何かしらもう少しの工夫がしてあるのかもしれません。私が行った変更を以下に掲載しておきます)
instance NFData (REGW c s) where rnf (REGW e f r) = rseq e `Prelude.seq` rseq f `Prelude.seq` rnf r instance NFData (REW c s) where rnf EPSW = () rnf (SYMW _) = () rnf (ALTW a b) = rnf a `Prelude.seq` rnf b rnf (SEQW a b) = rnf a `Prelude.seq` rnf b rnf (REPW r) = rnf r
matchW :: Semiring s => REGW c s -> -> s
matchW r [] = emptyW r
--matchW r (c : cs) =
-- finalW (foldl (shiftW zero . regW) (shiftW one (regW r) c) cs)
matchW r (c : cs) =
let nr = shiftW one (regW r) c in
rnf nr `Prelude.seq` go nr cs
where
go !r [] = finalW r
go !r (c:cs) =
let nr = shiftW zero (regW r) c in
rnf nr `Prelude.seq` go nr cs
無限正規表現
シンプルでエレガントで、しかも高性能な正規表現マッチャが書けました。しかし、正規表現は当たり前ですが、正規言語しかマッチすることができません(実際には広く用いられているpcreなどの正規表現ライブラリでは、後方参照などの拡張により正規言語を超える範囲の言語を扱えたりします)。正規言語ではない言語は、例えば簡単な例ですと、正しく対応する括弧、(())や()()()にマッチして、())や)()(にマッチしないようなものがあります。
もっとシンプルな例だと、aとbが同じ個数だけ並んだ文字列を表す言語
{ a{n}b{n} | n>=0 }
が正規言語ではありません。これは正規言語よりも強力なクラス、文脈自由言語に含まれます。bの列をパーズする際に、直前にaを何個読んだか憶えておかなければなりません。しかし、有限のオートマトンでは、これを任意のnに対して行うことはできないのです。
つまり、正規表現が受理できる言語の範囲を正規言語に至らしめているのは、オートマトンのサイズが有限、即ち正規表現のサイズが有限であることに原因があります。では、その制約を外した、例えば無限のサイズの正規表現というものは考えられないでしょうか。Haskellの遅延評価を用いると、無限正規表現というものを実際に作ることが出来ます。
無限の正規表現が許されると、先程の言語 { a{n}b{n} | n>=0 } は、無限正規表現を用いて
ε | ab | aabb | aaabbb | ...
と表せます。これは冗長なので共通部分を括ると、
ε | a (ε | a (ε | a (...) b) b) b
となります。これをHaskellで記述すると、
let a = symW ('a'==)
let b = symW ('b'==)
let anbn = altW epsW (seqW a (seqW anbn b))
こうなります。anbn が再帰していますが、遅延評価のおかげで正しく定義できます。
さてこれをマッチャに食わせてみます。
ghci> matchW anbn "" ... (止まらない)
残念ながらこのままでは停止しません。これは、finalの実装が正規表現ツリーを全てトラバースするようになっているため、せっかくの遅延評価の意味が無くなっているためです。実際にはfinalはツリーの全てを見る必要はありません。というのも、初期状態では全てのノードのfinalはzeroになっていて、step毎に非zeroが増えていきますが、その数は有限stepでは有限個しか無いためです。必ずzeroであると分かっている場所はトラバースする必要はないのです。
トラバースする必要のないノードを省くために、REGW型にサブツリーのいずれかが非zeroである可能性があるかどうかを示すBoolのメンバactiveを追加します。
data REGW c s = REGW { active :: Bool,
emptyW :: s,
finalW :: s,
regW :: REW c s }
スマートコンストラクタをactiveに対応させます。
epsW :: Semiring s => REGW c s
epsW = REGW { active = True,
emptyW = one,
finalW = zero,
regW = EPSW }
symW :: Semiring s => (c -> s) -> REGW c s
symW f = REGW { active = True,
emptyW = zero,
finalW = zero,
regW = SYMW f }
altW :: Semiring s => REGW c s -> REGW c s -> REGW c s
altW p q =
REGW { active = active p || active q,
emptyW = emptyW p <+> emptyW q,
finalW = finalA p <+> finalA q,
regW = ALTW p q }
seqW :: Semiring s => REGW c s -> REGW c s -> REGW c s
seqW p q =
REGW { active = active p || active q,
emptyW = emptyW p <*> emptyW q,
finalW = finalA p <*> emptyW q <+> finalA q,
regW = SEQW p q }
repW :: Semiring s => REGW c s -> REGW c s
repW r =
REGW { active = active r,
emptyW = one,
finalW = finalA r,
regW = REPW r }
finalWの代わりに先に active を見るfinalA関数を定義します
finalA :: Semiring s => REGW c s -> s finalA r = if active r then finalW r else zero
finalWはfinalA越しに再帰していますが、どこかでactiveがFalseになることにより再帰が終了します。これで無限正規表現を正しく扱えるようになりました。また、余分なトラバースが避けられるので、普通の正規表現を処理する際にも高速化に繋がります。
finalを見るときに、先にactiveを参照するようにしましたが、今度はactiveフィールドが無限に再帰します。なので、最初にactiveフィールドをトラバースせずに作る必要があります。最初の正規表現ツリーの状態は、全てのノードの重みがzeroなので、activeはFalseにしておけば良いです。これのためのスマートコンストラクタを作ります。
alt :: Semiring s => REGW c s -> REGW c s -> REGW c s
alt p q =
REGW { active = False,
emptyW = emptyW p <+> emptyW q,
finalW = zero,
regW = ALTW p q }
seq :: Semiring s => REGW c s -> REGW c s -> REGW c s
seq p q =
REGW { active = False,
emptyW = emptyW p <*> emptyW q,
finalW = zero,
regW = SEQW p q }
rep :: Semiring s => REGW c s -> REGW c s
rep r =
REGW { active = False,
emptyW = one,
finalW = zero,
regW = REPW r }
最後に、shiftW関数をactiveに対応させます。
shiftW :: (Eq s, Semiring s) => s -> REGW c s -> c -> REGW c s shiftW m r c | active r || m /= zero = stepW (regW r) c | otherwise = r
既存のshiftWはstepWにリネームしておきます。
これで完成です。
ghci> matchw anbn "" True ghci> matchw anbn "ab" True ghci> matchw anbn "aabb" True ghci> matchw anbn "aabbb" False
さてこの無限正規表現はどの程度の力を持つのでしょうか。任意の文脈自由言語が解析できるのでしょうか。これは左再帰を除去してやれば可能なように思われます。文脈自由文法がグライバッハ標準形になっていれば、明らかにこれはHaskellの無限正規表現で記述可能です。全ての文脈自由文法はグライバッハ標準形に変換可能ですので、無限正規表現は任意の文脈自由言語を受理することができるということになります。
無限正規表現は文脈自由文法よりも強力なクラスを扱うことができるのでしょうか?例えば、次の言語の例は文脈自由文法では表現できない、文脈依存言語の例として知られています。
{ a{n}b{n}c{n} | n>=0 }
これも無限正規表現なら、
ε | abc | aabbcc | aaabbbccc | ...
として表現されます。これも同様にくくりだし、
ε | a (bc | a (bbcc | a (bbbccc | a (...))))
これをHaskellで記述すると
ghci> let bcs n = foldr1 seq (bs n ++ cs n) ghci> let a = symW (’a’==) ghci> let abc n = seq a (alt (bcs n) (abc (n+1))) ghci> let anbncn = alt epsw (abc 1)
こうなります。
ghci> matchw anbncn "" True ghci> matchw anbncn "abc" True ghci> matchw anbncn "aabbcc" True ghci> matchw anbncn "aabbbcc" False
文脈自由言語に入らない言語もマッチすることができました。さてこの無限正規表現はどのぐらい力を持つのでしょうか。私にはちょっと分かりかねるので、皆さん是非考えてみてください。
Appendix: ソースコードなど
本文で述べられた重みつき正規表現の実装が、Weighted RegExp Matchingとして公開されています。
また、weighted-regexpパッケージとして、hackageにアップロードされています。是非皆さん、実際に動かしてみて遊んでみてください。