Blog
本記事は、2019年インターンシップとして勤務した武田惇史さんによる寄稿です。
こんにちは。2019年PFN夏季インターンシップに参加した東京大学の武田惇史です。インターンでは、Optunaチームのもと、「効率の良いブラックボックス最適化手法の開発」というテーマに取り組みました。
概要
ブラックボックス最適化のアルゴリズムの一つに、ガウス過程に基づくベイズ最適化(GP-BO)があります。GP-BOは、局所解に陥りにくく、少ない探索回数で良い解を得ることができる手法として知られていますが、ナイーブな方法だと探索回数が増えたときに計算が非常に重くなってしまいます。
インターンでは、数万回の探索回数を想定した問題に対しGP-BOを適用するため、高速に動作するベイズ最適化手法を提案し、あるベンチマークテストに対して、過去のコンペティションで優勝したBIPOP-CMA-ESという手法より良い性能を出すことに成功しました。
はじめに
インターンでは、Optunaチームで「効率の良いブラックボックス最適化手法の開発」というテーマに取り組みました。
Optunaとは
Optunaは、PFNが開発しオープンソースとして公開しているハイパーパラメータ自動最適化フレームワークです。
ディープラーニングを例にとると、学習係数、バッチサイズ、中間層の数等、様々なハイパーパラメータが存在し、重み学習後のモデルの性能はハイパーパラメータによって異なります。この性能を最大化するハイパーパラメータを探索するのがハイパーパラメータ最適化であり、これを自動化するのがOptunaです。
ブラックボックス最適化(BBO)とは
ハイパーパラメータ最適化は、ブラックボックス最適化という問題として定式化されます。ブラックボックス関数とは、具体的な入力値に対する出力を見ることでしか情報を得られないような関数であり、これを最大化(最小化)するのがブラックボックス最適化(BBO)です。
図:ブラックボックス関数f。入力と出力は見えるが、出力が得られる過程は不明
ベイズ最適化
BBOの手法として近年注目されているのがベイズ最適化です。ベイズ最適化では、評価済みの関数値から未知の入力に対する予測値(の確率分布)を算出し、それに基づいて次に評価する点を決定します。この確率分布は、ベイズ推定における予測分布に対応します。任意の入力に対する出力値の予測分布を求めるため、関数の予測分布を求めていると言うことができます。この関数の予測分布を求めるのに、ベイズ最適化ではガウス過程回帰が一般に用いられます。
ガウス過程回帰は、任意のN点の出力値の同時分布がガウス分布であり、それらのうちのどの2点の入力に対応する出力値の共分散も、その2点の入力値の関数(カーネル関数と呼ばれる)として表されるという仮定に基づいて、未知の入力に対する出力の予測分布をガウス分布として求めます。近い入力同士ほどそれらの出力の相関が強いことを表すようなカーネル関数を用いることで関数の滑らかさに関する制約をソフトに(確率的に)表現することができます。
ガウス過程回帰で正確に関数値を予測するには、カーネル関数をどう設計するかが重要になります。ブラックボックス関数に対しては、関数に対する事前知識がないので、パラメタライズされたカーネル関数を用い、そのパラメータを学習することで対応します。学習においては、周辺尤度最大化や交差検証などを基準に最適化問題として定式化し、ニュートン法やMCMCなどのアルゴリズムが用いられます。
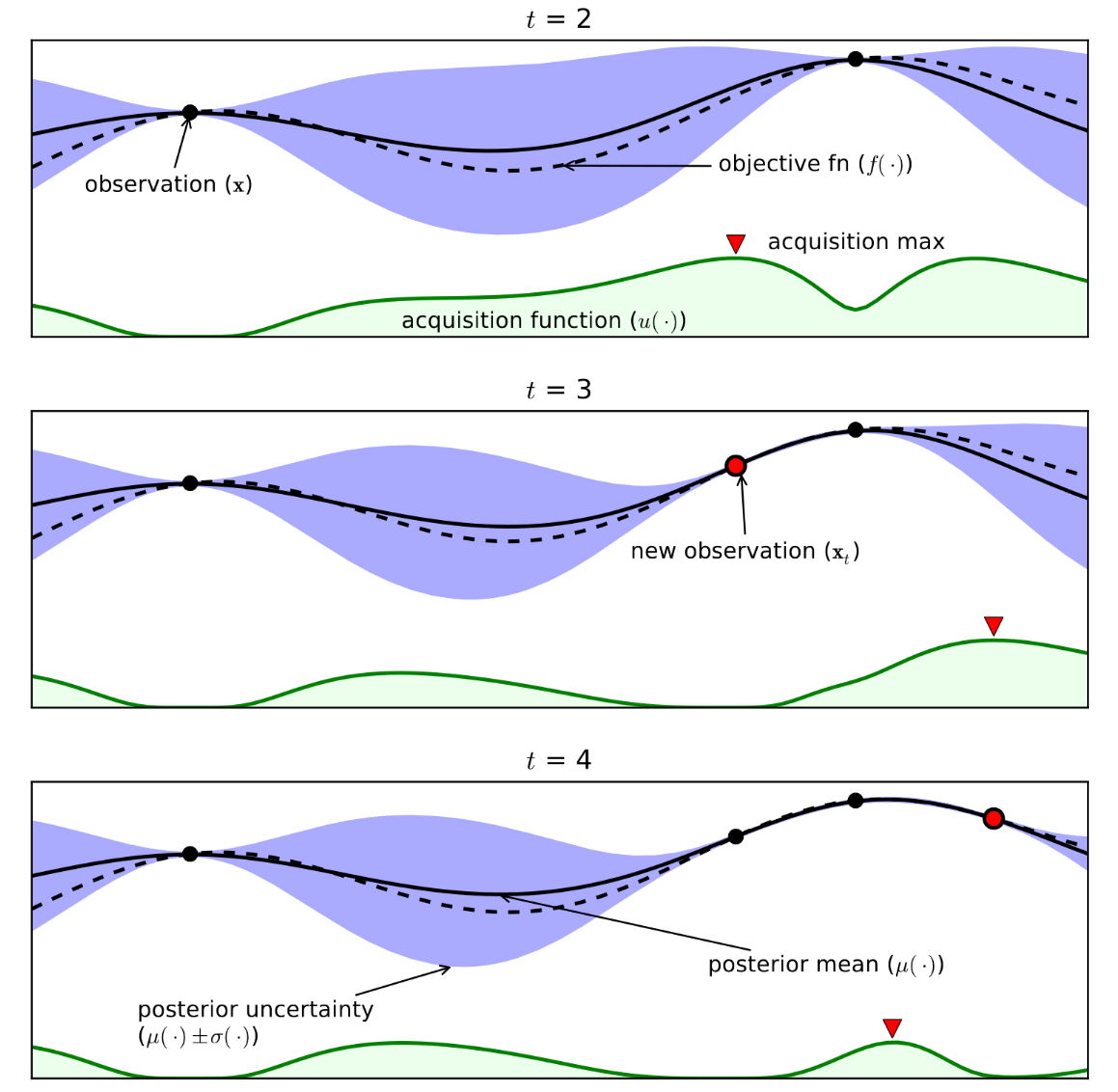
図:1次元上のベイズ最適化の動作例[1]
インターン課題
GP-BOは局所解に陥りにくく、少ない探索回数で良い解を得ることができる手法として知られています。しかし、適切にカーネル関数が設定されていないと入力変数間のスケールの違いに対応できず、非効率な探索となります。その一方で、適切なカーネル関数を推定させるためには多くの計算時間が必要となります。
もし適用対象がディープラーニングのハイパーパラメータ最適化であれば、一回の関数評価は一回の学習に相当し、関数評価に時間がかかるため、関数評価の回数はせいぜい数十回から数百回であり、計算が重いというデメリットは問題になりません。しかし、Optunaのユースケースには関数評価に時間がかからず、数万回探索可能な問題設定もあります。このような場合にGP-BOを適用すると、GP-BO自体がボトルネックとなり、現実的な時間では計算を終えることができません。
そこで、探索範囲を優秀なサンプルに限定することで数万回の探索が可能であるような最適化手法を考案しました。
GP-BOの課題
GP-BOでは、探索回数を\(N\)としたとき、ガウス過程における学習・推論時に必要なN×N行列の逆行列の計算を\(N\)ステップ行います。この際、Sherman-Morrisonの公式により、逆行列を1ステップ\(O(N^2)\)の計算量で求めることができ、全体で\(O(N^3)\)かかってしまいます。そのうえ、性能を出すためにはカーネル関数やパラメータを学習する必要があり、カーネル関数のパラメータが変わると逆行列を求める行列全体の値が変わるためSherman-Morrisonの公式が使えず、逆行列の差分計算を効率的にすることが難しくなるため、計算量は\(O(N^4)\)となります。
性能を出すために重要なパラメータが変数のスケールに関するパラメータです。もし関数の入力変数間のスケールが大きく異なる場合、カーネル関数として通常のユークリッド距離のみに依存するものを選んでいたとすると、本来影響の少ない方向からの影響を大きく見積もり、関数の予測が上手く動きません。変数間の相関やスケールの違いに対応するには、カーネル関数に多くのパラメータを設定し、それをメタレベルの最適化問題を解くことによって調整する必要があります。場所によってスケールが異なる性質(悪スケール性)を持つ関数に対しては、より複雑なカーネル関数のパラメータを適切に学習する必要が生じ、さらに計算量が増えます。
提案手法
Limited-GP
提案手法ではこの点を解決するため、ガウス過程で参照するサンプル点を制限します。
まず、これまで探索した点から上位\(K\)点に対する平均ベクトルと共分散行列を求めます。求めた平均ベクトルと共分散行列が定める各点へのマハラノビス距離を計算します。距離が小さい方から\(K\)番目の点を通る(マハラノビス距離での)超球の内部に限って獲得関数が最も良くなる値の探索を行い、次の探索点を決めます。獲得関数は、距離が小さい方から\(2K\)個の点のみを参照したときのガウス過程回帰の結果に基づいて計算されます。カーネル関数としては2点間のマハラノビス距離が遠いほど値が指数的に小さくなるようなものを選びます。遠くの点の影響が小さいので、参照点を近い方から\(2K\)個に限れば十分となります。
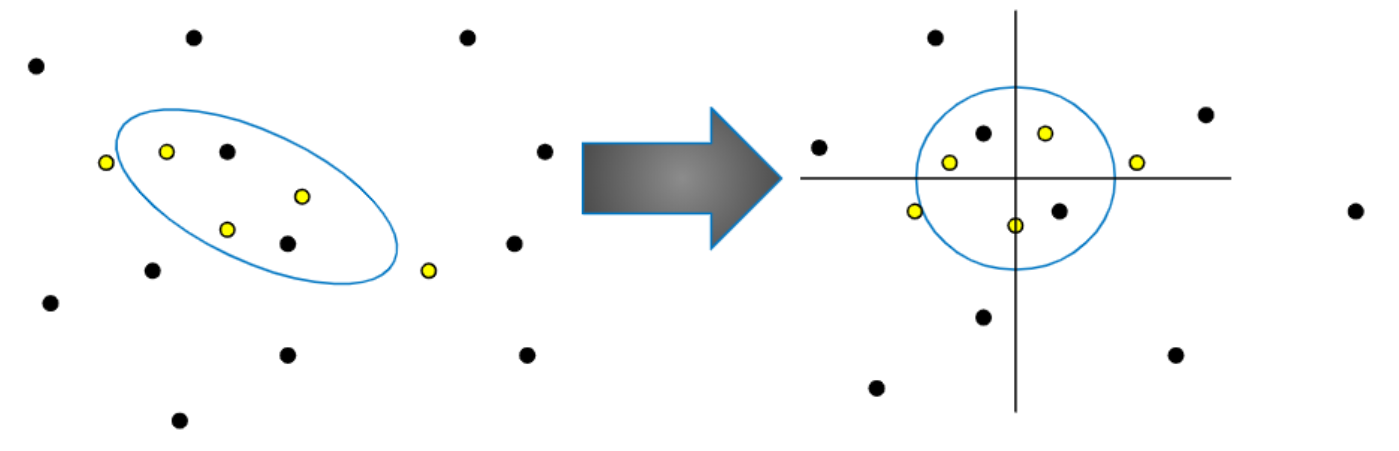
図:マハラノビス距離を原点からのユークリッド距離に対応させる線形変換。黄色い点はK=5としたとき関数値の評価が最も良かったK点を表す。変換後、図に収まらない点は省略している。
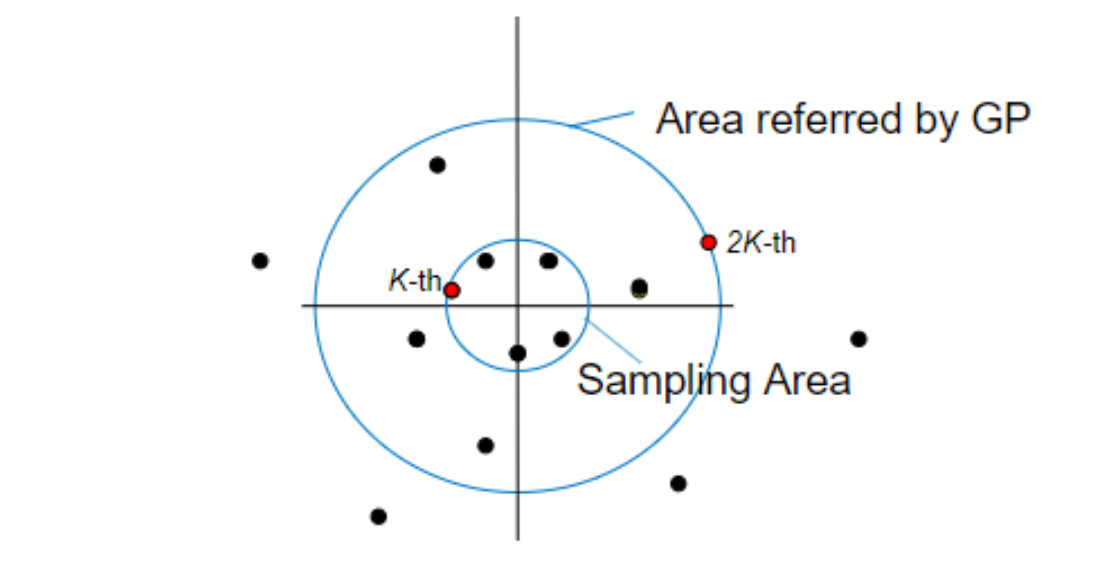
図:ガウス過程において参照する点の範囲(外側の円)とサンプルを得る範囲(内側の円)
上位\(K\)点に対する平均ベクトルと共分散行列に基づくマハラノビス距離における円は、それまでに見つかった最適値付近における関数の等高線を楕円形に近似したものと考えられます。すなわち、このマハラノビス距離が通常のユークリッド距離になるように空間を変換すると、等高線は正円に近くなると考えられます。このため、関数は等方性(方向によって性質が変化しない性質)を得ることができ、ガウス過程のカーネルパラメータを用いたスケールの調整が不要になります。
これまでに探索した点の数が一定値を超えた場合、新たに探索点が増えるたびに対応する関数値が最も悪い点の情報を捨てます(これにより性能が落ちないことは実験的に確かめています)。こうすることで、参照点全体の個数が定数個で抑えられ、1ステップの計算量は\(O(1)\)となり、Nステップでは\(O(N)\)となりますので、ナイーブなGP-BOにおける\(O(N^4)\)と比べ、大きく改善します。
再スタート戦略
Limited-GPで制限される探索範囲は、実験上多くの場合でだんだんと狭まっていきます。そのため、多峰な関数では一度局所解に陥るとそこから抜け出すことは困難です。
そこで、本手法ではLimited-GPを繰り返し行うことで大域的な最適解の発見を試みます。この際、Limited-GPへの初期値として与えられる平均ベクトルと共分散行列をCMA-ES[2]というアルゴリズムのrank-μ-updateを参考にした方法で適応させます。具体的には、毎ステップ、それまでにLimited-GPが発見した解のうち特に良かった点に対する共分散行列を求め、その移動平均を用いて次のLimited-GPへの初期値を決定します。CMA-ESベースの方法によって、平均ベクトルと共分散行列は関数の細かいノイズを無視したときの大域的な構造を学習します。
動作の様子
以下に50回の探索点をプロットを載せます。数字は探索順を示します。また、明るいところほど良い解であることを示しています。
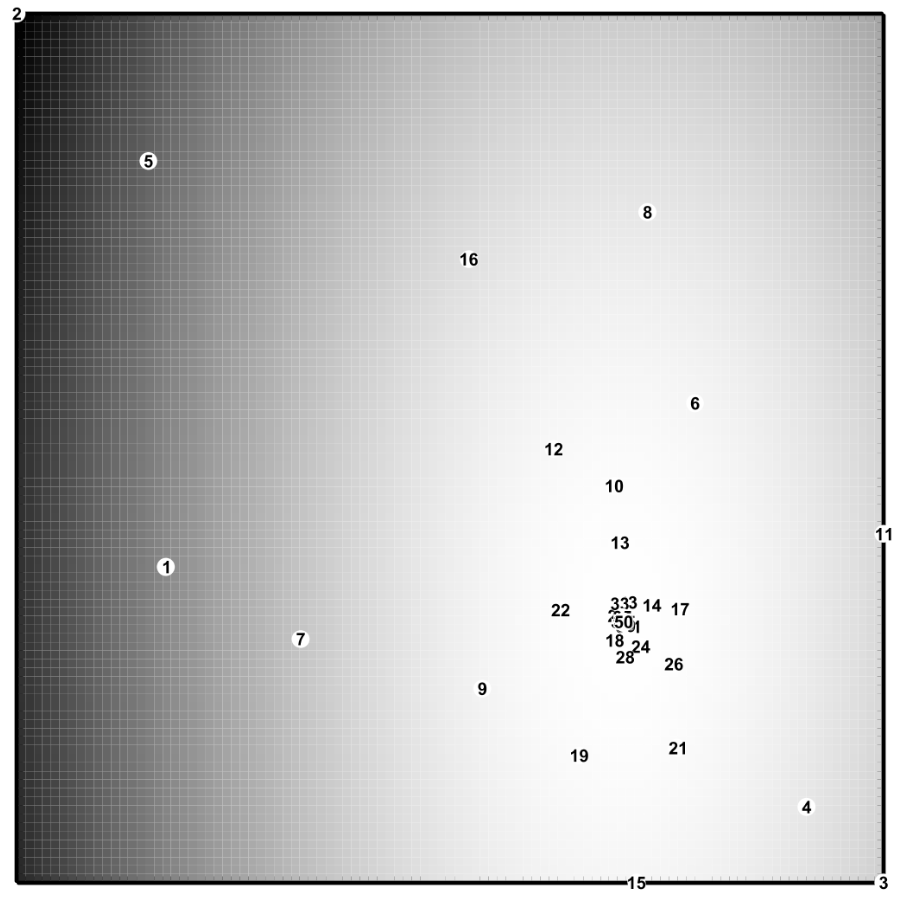
徐々に探索位置が最適解へと近づき、50ステップのうちに最適解へ収束していることが分かると思います。
続いて、入力変数間に相関があるような関数に対する探索範囲の変遷について見ます。
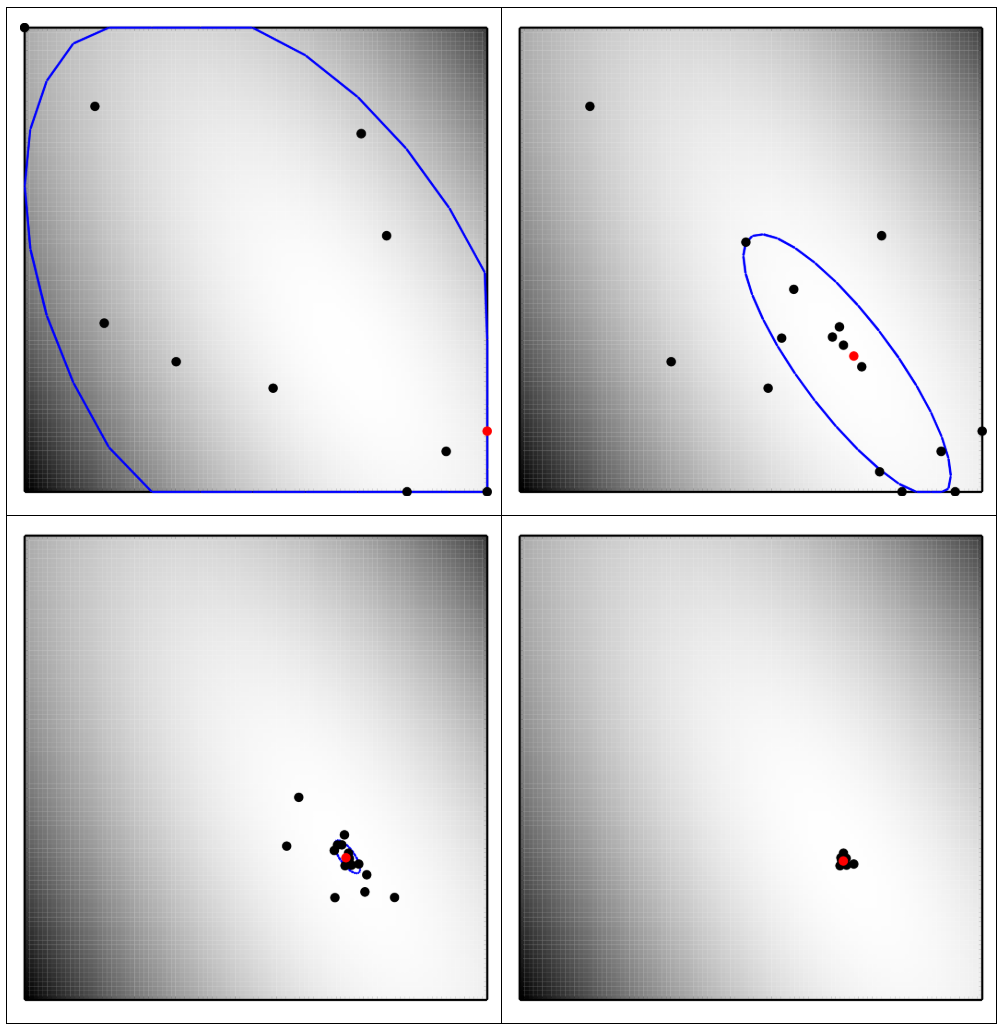
10ステップの図を示しています。この図では青い線が探索領域を表し、黒い点がガウス過程で参照される点を示し、赤い点が新たにサンプルされた点を表します。探索範囲が等高線に添うように変形しつつ、最適解へと収束していることが分かります。
次に、多峰関数(Rastrigin関数)に対して、再スタートの度に最適解へ収束しやすくなっていることを確認します。
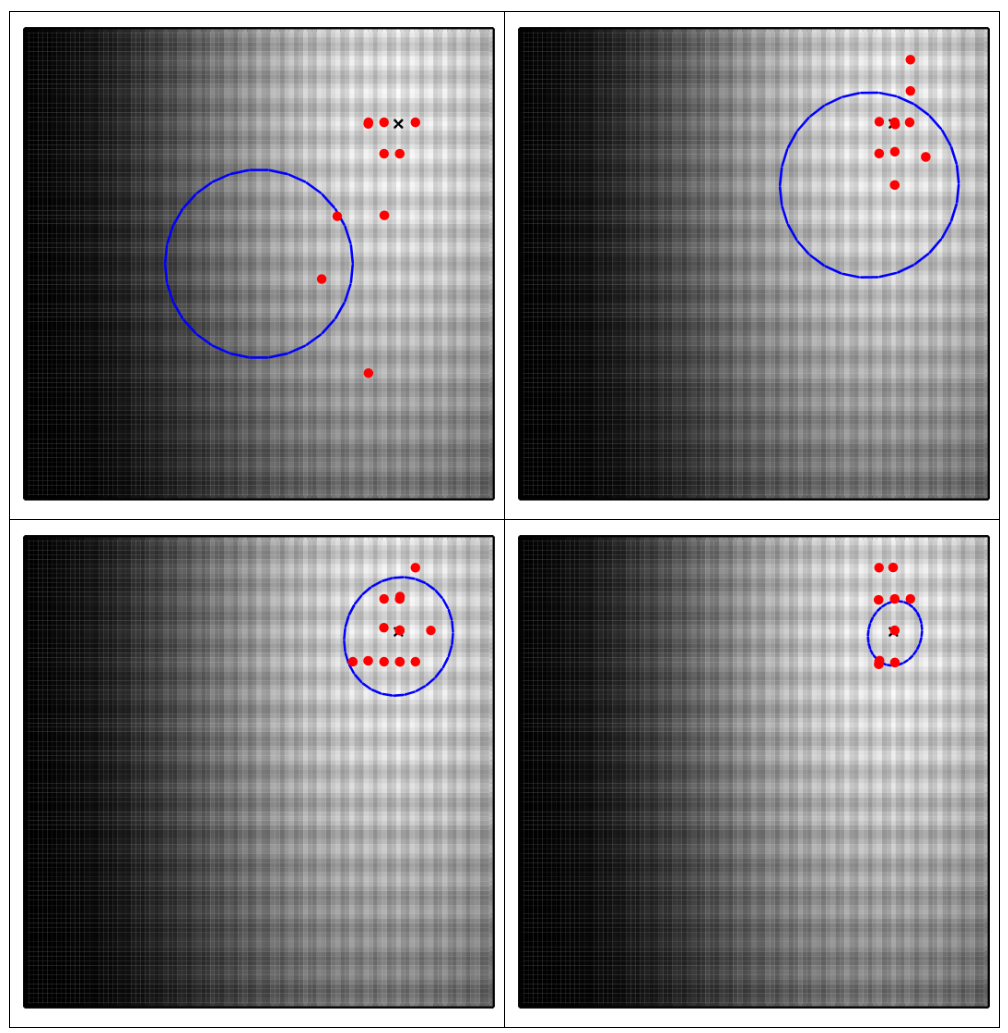
10ステップおきの図を取っています。×印が最適解を示します。また、青い線がLimited-GPの初期値として入力される平均ベクトルと共分散行列が規定するマハラノビス距離上の半径1の円を示し、赤い点が直近10回のLimited-GPが発見した最良点を示しています。青い線は最適解へ収束していき、Limited-GPの到達点も最適値付近へ収束していることが分かります。
ベンチマーク
データセット
COCO(COmparing Continuous Optimisers)と呼ばれるベンチマークを使ってテストをしました。COCOは2009年より使われているブラックボックス最適化用のベンチマークで、次元数を自由に変更できるような関数を24種類、360個提供しています。毎年コンペティションが開かれており、多くの手法が試されています。
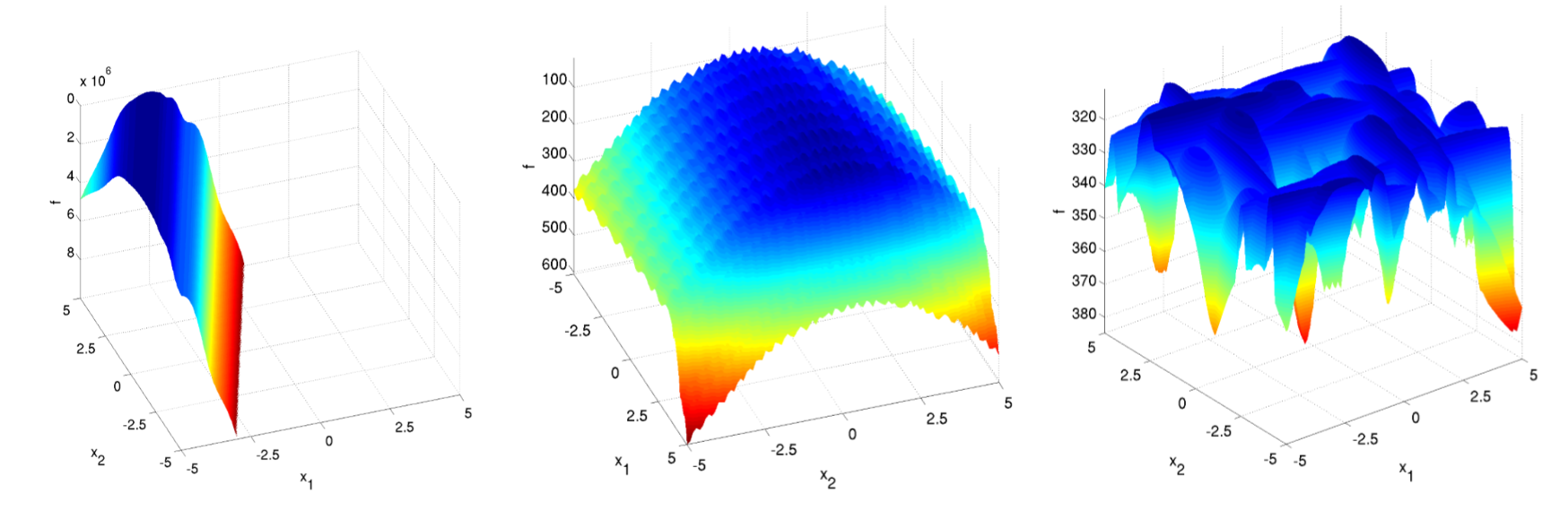
図:COCOが提供する関数群の一部
実験設定
手法のハイパーパラメータについては、\(K=7+3logD\)(\(D\)は目的関数の入力次元数)と定め、カーネル関数はガウスカーネル、獲得関数はLCBに固定します。
関数の次元数\(D\)は\(D=2\)と\(D=3\)でそれぞれ実験しました。探索回数は\(10^4×D\)としました。
結果
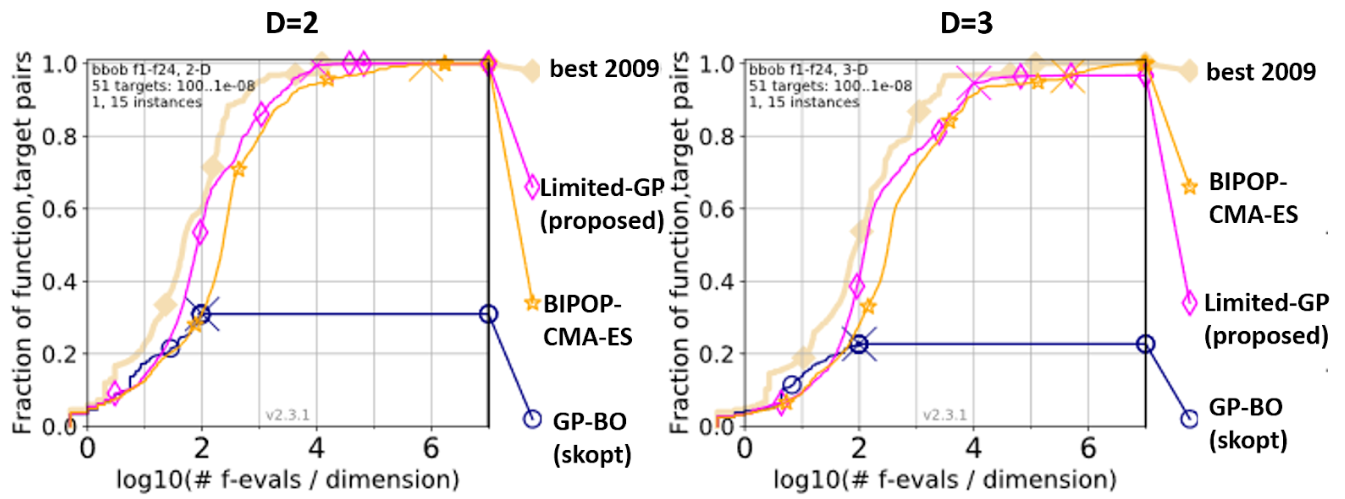
図:ベンチマーク結果
結果が上図になります。左は2次元、右は3次元での結果で、横軸がlog(探索回数/次元数)を表し、縦軸がすべての関数に対する平均精度を表します(※正確には、このグラフはempirical cumulative distribution function [3]と呼ばれるものです)。グラフ上の×印は探索の終了点を表し、それより後の部分は、結果描画時に補完された値となります(詳細は参考文献を参照して下さい)。
”Limited-GP(proposed)”が提案手法を表しています。”BIPOP-CMA-ES”はBBOにおいて有望視されている手法であるCMA-ESの亜種で、2009年のコンペティションで最も高い性能を出した手法であり、総合的に最も強い手法と言われています[4]。”GP-BO(skopt)”はBBO用pythonライブラリで、GP-BOの実装であるscikit-optimize(skopt)の結果になります。skoptは非常に実行時間がかかるため、探索回数は100×(次元数)回で、一部の関数インスタンスに対してのみベンチをとっており、あくまで参考までに比較として載せています。また、”best 2009”は各関数ごとに2009年のコンペティションで提出された手法のうち最も良い結果が得られたものを選んだ場合の学習曲線を表しています。実際にはブラックボックス関数であるため手法をあらかじめ選ぶということはできず、ある種の性能上界として参考までに載せています。
提案手法はBIPOP-CMA-ESと比べても効率良く探索できるという結果が得られました。
なお、今回はインターン期間が限られているという制約もあり、低次元関数のみに対象を絞って開発・検証を行いました。高次元関数においては、まだBIPOP-CMA-ESの方が良い性能を示すことが確認できており、そこでの最適化性能の向上は今後の課題となります。
まとめ
今回のインターンでは、ガウス過程に基づくベイズ最適化を改良したLimited-GPと再スタート戦略の組み合わせを提案し、過去のベンチマークテストにて高い性能を出すことができました。
本手法の実装はhttps://github.com/pfnet-research/limited-gpで公開されています。
参考文献
[2] Hansen, N.: The CMA Evolution Strategy: A tutorial.
メンターからのコメント
メンターを担当したPFNの太田と柳瀬です。
昨年12月にOSSとしてリリースしてから、Optunaの応用は広がっており、当初想定していた機械学習のパラメータ最適化だけではなく、ブラックボックス最適化のソルバとしても使われるようになってきました。
そうした状況のもとで、武田さんにはブラックボックス最適化のソルバの調査と改善に取り組んでいただきました。学会発表が重なるなど,必ずしも時間が十分だったわけではありませんが,武田さんは次々とアイデアを出して、限定的な評価環境ではありますが計算が軽くて探索性能の良いソルバの可能性を示してくれました。
Optunaではライブラリの機能開発だけではなく、こうした将来に向けての研究開発も引き続き行っていきます。興味のある学生の皆さんは、ぜひ来年のPFNインターンシップへの応募を検討ください。もちろん、中途・新卒での人材募集も通年で行っていますので、こちらも興味のある方はぜひご検討ください。PFNの人材募集のページはこちらです。




